Dynamic programming - memorisation
DP
Dynamic programming (DP) is a method for solving complex problems by breaking the original problem down into smaller, overlapping subproblems.
Memoization is one of the techniques to implement DP. The core idea of memoization is: store the results of function calls, and when the same inputs appear again, directly look up the stored results instead of recalculating.
In practice, this is usually done with a mapping (a dict in Python) or another data structure as a cache to avoid redundant calculations and improve efficiency.
You can imagine it like a calculator with memory. If you ask it 5 x 7, it will compute and store the result 35. The next time you ask the same input, the calculator will directly fetch 5 x 7 = 35 from memory instead of recalculating.
Unoptimized Fibonacci
As an example, let’s compute the Fibonacci sequence without memoization:
def fib(n):
if n <= 1:
return n
return fib(n-1) + fib(n-2)
If we visualize this approach, it looks like a tree:
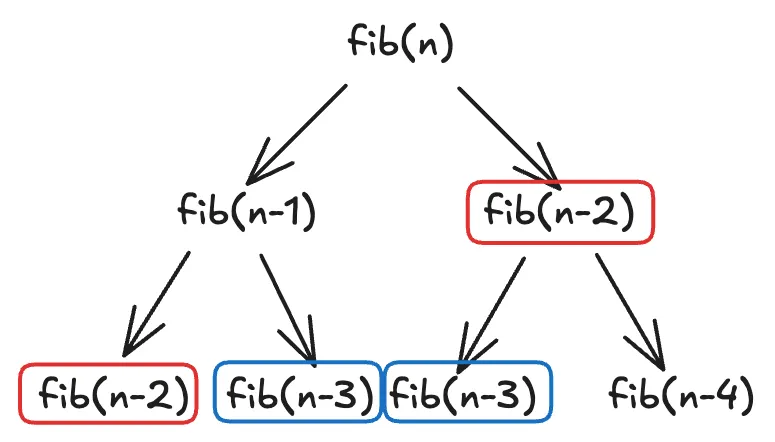
figure1. fib visualization
Looking closely, we can see many repeated computations in this tree (highlighted in red and blue boxes).
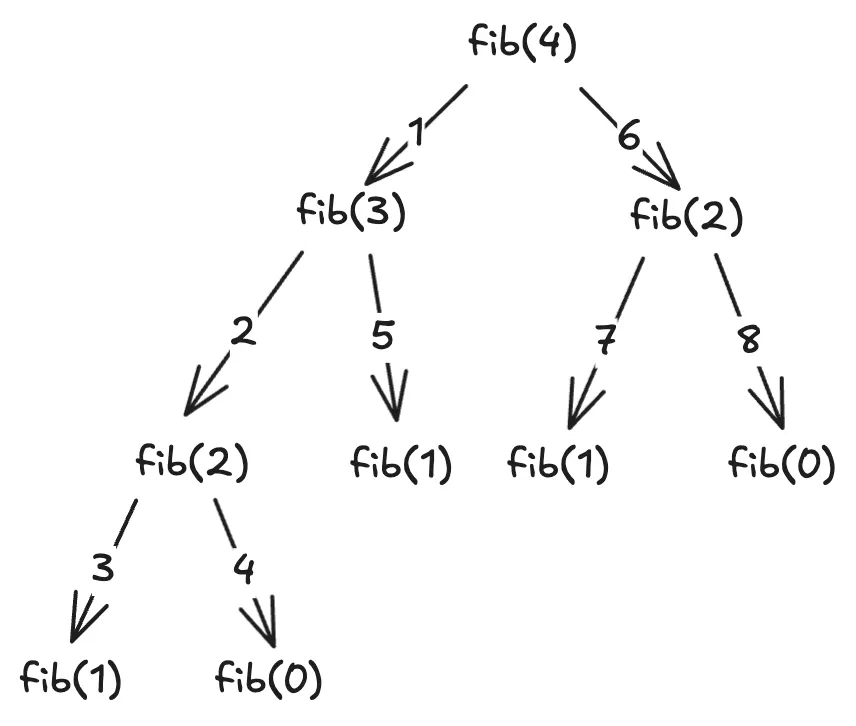
figure2. fib(4) visualization
For instance, in fib(4), the function calls proceed as follows:
| Step | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Input | 3 | 2 | 1 | 0 | 1 | 2 | 1 | 0 |
| Repeated? | ✅(3) | ✅(2) | ✅(3) | ✅(4) |
We can see that at steps 5–8 (fib(1), fib(2), fib(1), fib(0)), these calculations had already been done earlier. This means the algorithm is repeating the same computation many times.
Optimized Fibonacci
If we record the results of already-computed calls, wouldn’t that save a lot of work? (Yes!)
A more efficient solution is to use a mapping (dictionary in Python) to store computed results:
def mfib(n, memo={}):
if n in memo:
return memo[n]
if n <= 1:
return n
memo[n] = mfib(n-1, memo) + mfib(n-2, memo)
return memo[n]
In the same example (fib(4)), the repeated calculations (steps 5–8) are avoided because when reaching if n in memo:, we can just return the stored result instead of recalculating.
Complexity Analysis
You might wonder: How much time does memoization actually save?
-
Unoptimized Fibonacci:
The recursion tree has height n (to reach the base case, you need n levels). For fib(4), the recursion tree has 9 nodes, approximately 2^4. In general, the total number of nodes is 2^n, so the time complexity is O(2^n).
-
Optimized Fibonacci (with memoization):
We only compute when the input hasn’t been stored yet. In total, we calculate fib(n-1), fib(n-2), …, fib(1) — about n-1 calls. So the time complexity is O(n).
-
Space complexity consideration:
Taking fib(4) as an example, recursion depth is n. The maximum stack depth is n, so the space complexity is O(n).
Thus, memoization reduces time complexity dramatically, from exponential to linear.
Script for Comparison
Here’s a small script to count how many times each approach calculates fib(n-1) + fib(n-2):
cnt = 0
mcnt = 0
def fib(n):
global cnt
if n <= 1:
return n
cnt += 1
return fib(n-1) + fib(n-2)
def mfib(n, memo={}):
global mcnt
if n in memo:
return memo[n]
if n <= 1:
return n
mcnt += 1
memo[n] = mfib(n-1, memo) + mfib(n-2, memo)
return memo[n]
fib(1 << 5)
mfib(1 << 5)
print(f"fib function calculated f(n-1) + f(n-2) {cnt} times")
print(f"mfib function calculated f(n-1) + f(n-2) {mcnt} times")
Output:
fib function calculated f(n-1) + f(n-2) 3524577 times
mfib function calculated f(n-1) + f(n-2) 31 times
Memoization reduces 3,524,577 recursive calculations down to only 31 calculations — a huge improvement.